ABC公司有一个锆石矿,目前还有2年的开采量,但要正常运行预计需要再追加投资600万元;若立刻变现可售1000万元,其他相关资料如下:
(1)矿山的产量每年约100吨,锆石目前价格为每吨10万元,预计单价每年上涨8%,但是很不稳定,其标准差为14%。
(2)营业的付现固定成本每年稳定在300万元。
(3)1~2年后矿山的残值分别为800万元、200万元。
(4)含有风险的必要报酬率为10%,无风险报酬率为5%。
(5)为简便起见,忽略其他成本和税收问题。
要求:
(1)假设项目执行到项目周期期末,计算不含期权的项目净现值(计算结果填入下方表格中,不用列出计算过程)(精确到0.0001万元),并判断是否放弃执行该项目。
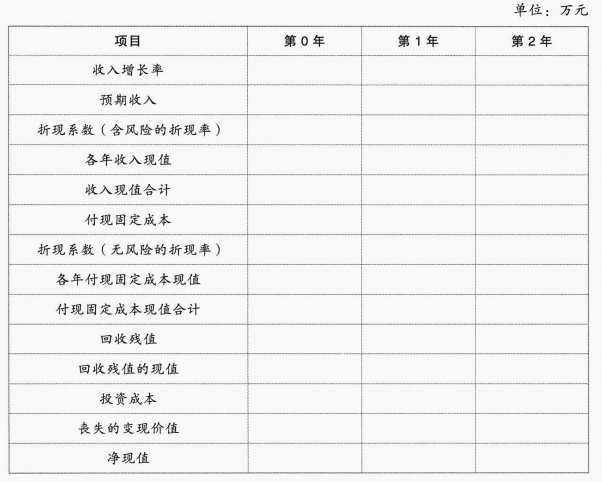
(2)要求采用二叉树方法计算放弃决策的期权价值(计算结果填入下方表格中,不用列出计算过程)(上行概率和下行概率保留4位小数,其余结果精确到0.01),并判断是否放弃执行该项目。
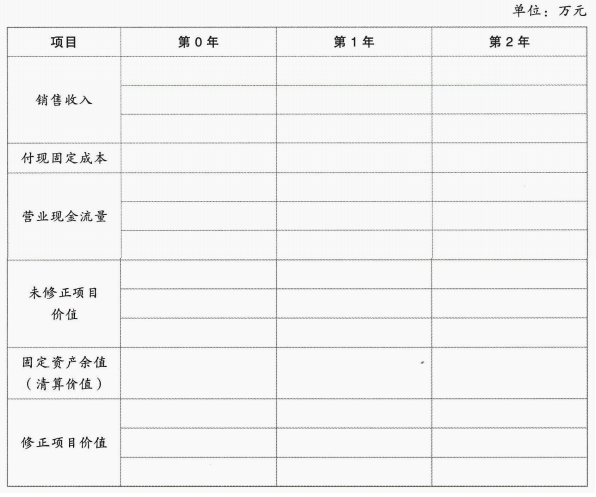
(1)矿山的产量每年约100吨,锆石目前价格为每吨10万元,预计单价每年上涨8%,但是很不稳定,其标准差为14%。
(2)营业的付现固定成本每年稳定在300万元。
(3)1~2年后矿山的残值分别为800万元、200万元。
(4)含有风险的必要报酬率为10%,无风险报酬率为5%。
(5)为简便起见,忽略其他成本和税收问题。
要求:
(1)假设项目执行到项目周期期末,计算不含期权的项目净现值(计算结果填入下方表格中,不用列出计算过程)(精确到0.0001万元),并判断是否放弃执行该项目。

(2)要求采用二叉树方法计算放弃决策的期权价值(计算结果填入下方表格中,不用列出计算过程)(上行概率和下行概率保留4位小数,其余结果精确到0.01),并判断是否放弃执行该项目。

正确答案:
(1)
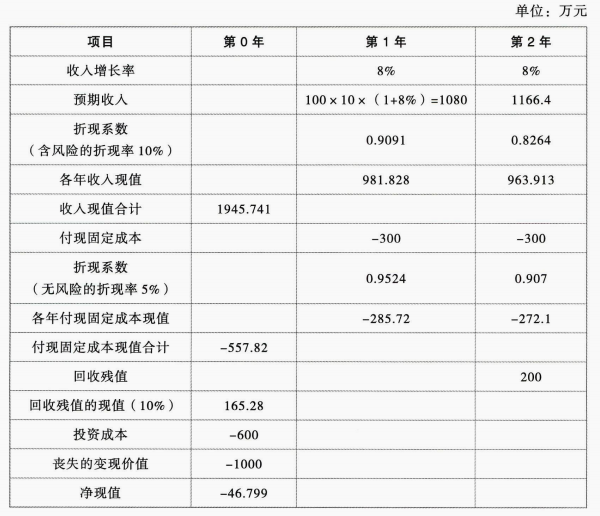
因不含期权的项目净现值小于0,故应放弃执行该项目。
(2)
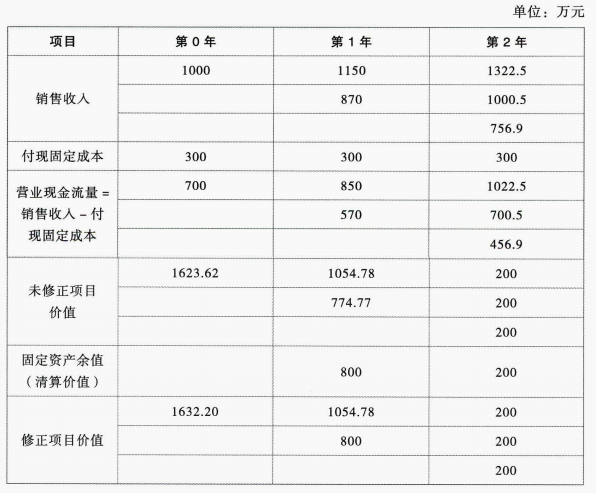
含有期权的项目净现值=1632.20-600-1000=32.20(万元)
期权的价值=32.20-(-46.799)=79.00(万元)
因此应当进行该项目,不应放弃。但如果价格下行使得销售收入等于或低于870万元时,应放弃该项目,进行清算。

因不含期权的项目净现值小于0,故应放弃执行该项目。
(2)

含有期权的项目净现值=1632.20-600-1000=32.20(万元)
期权的价值=32.20-(-46.799)=79.00(万元)
因此应当进行该项目,不应放弃。但如果价格下行使得销售收入等于或低于870万元时,应放弃该项目,进行清算。
答案解析:
①确定上行乘数和下行乘数:
由于锆石价格的标准差为14%,所以:

d=1/u=1/1.15=0.87
②构造销售收入二叉树:
按照计划产量和当前价格计算
销售收入=100×10=1000(万元)
第1年的上行销售收入=1000×1.15=1150(万元)
第1年的下行销售收入=1000×0.87=870(万元)
第2年的二叉树以此类推。
③构造营业现金流量二叉树:
由于付现固定成本每年为300万元,销售收入二叉树各节点减去300万元,可以得出营业现金流量二叉树。
④确定上行概率和下行概率:
上行概率=(1+5%-0.87)/(1.15-0.87)=0.6429
下行概率=1-上行概率=1-0.6429=0.3571
⑤第2年末修正及未修正项目的价值均为200万元,因为到寿命终结必须清算。
第1年末上行未修正项目的价值=[(1022.5+200)×0.6429+(700.5+200)×0.3571]/(1+5%)=1054.78(万元)
第1年末下行未修正项目的价值=[(700.5+200)×0.6429+(456.9+200)×0.3571]/(1+5%)=774.77(万元)
0时点未修正项目的价值=[(850+1054.78)×0.6429+(570+774.77)×0.3571]1(1+5%)=1623.62(万元)
第1年末上行修正项目的价值=1054.78万元
第1年末下行修正项目的价值=800万元(即选择清算)
0时点修正项目的价值=[(850+1054.78)×0.6429+(570+800)×0.3571]/(1+5%)=1632.20(万元)。
由于锆石价格的标准差为14%,所以:

d=1/u=1/1.15=0.87
②构造销售收入二叉树:
按照计划产量和当前价格计算
销售收入=100×10=1000(万元)
第1年的上行销售收入=1000×1.15=1150(万元)
第1年的下行销售收入=1000×0.87=870(万元)
第2年的二叉树以此类推。
③构造营业现金流量二叉树:
由于付现固定成本每年为300万元,销售收入二叉树各节点减去300万元,可以得出营业现金流量二叉树。
④确定上行概率和下行概率:
上行概率=(1+5%-0.87)/(1.15-0.87)=0.6429
下行概率=1-上行概率=1-0.6429=0.3571
⑤第2年末修正及未修正项目的价值均为200万元,因为到寿命终结必须清算。
第1年末上行未修正项目的价值=[(1022.5+200)×0.6429+(700.5+200)×0.3571]/(1+5%)=1054.78(万元)
第1年末下行未修正项目的价值=[(700.5+200)×0.6429+(456.9+200)×0.3571]/(1+5%)=774.77(万元)
0时点未修正项目的价值=[(850+1054.78)×0.6429+(570+774.77)×0.3571]1(1+5%)=1623.62(万元)
第1年末上行修正项目的价值=1054.78万元
第1年末下行修正项目的价值=800万元(即选择清算)
0时点修正项目的价值=[(850+1054.78)×0.6429+(570+800)×0.3571]/(1+5%)=1632.20(万元)。
